Advertisements
Advertisements
प्रश्न
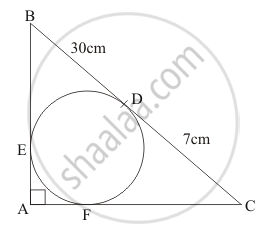
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.
उत्तर
Let us join the point of contact E with the centre of the circle say O. Also, let us join the point of contact F with the centre of the circle O. Now we have a quadrilateral AEOF.
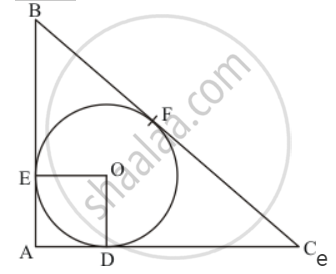
In this quadrilateral we have,
`∠EAD = 90^0`(Given in the problem)
`∠oda = 90^0`(Since the radius will always be perpendicular to the tangent at the point of contact)
`∠OEA = 90^0`(Since the radius will always be perpendicular to the tangent at the point of contact)
We know that the sum of all angles of a quadrilateral will be equal to `360^o`. Therefore,
`∠EAD + ∠ ODA + ∠ EOD + ∠ OEA = 360^o`
`90^0+90^o +90^o + ∠EOD = 360^o`
` ∠EOD = 90^o`
Since all the angles of the quadrilateral are equal to 90° and the adjacent sides are equal, this quadrilateral is a square. Therefore all the sides are equal. We have found that
AF = 5
Therefore,
OD = 5
OD is nothing but the radius of the circle.
Thus we have found that AF = 5 cm and radius of the circle is 5 cm.
APPEARS IN
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
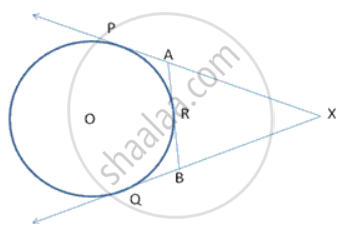
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
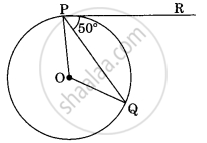
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.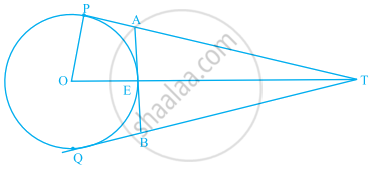
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
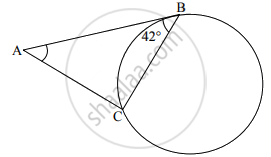
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
