Advertisements
Advertisements
प्रश्न
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
विकल्प
40 cm
9 cm
41 cm
50 cm
उत्तर
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is 40 cm.
Explanation:
Since tangent at a point on a circle is perpendicular to the radius through the point.
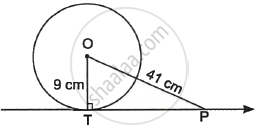
∴ ∠OTP = 90°
Now, In right-angled triangle OTP
OP2 = OT2 + TP2
(41)2 = 92 + TP2
TP2 = 1681 – 81
= 1600
TP = `sqrt(1600)`
= 40 cm
APPEARS IN
संबंधित प्रश्न
Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
How many tangents can be drawn to a circle from a point on it?
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
