Advertisements
Advertisements
प्रश्न
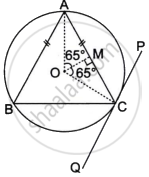
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
उत्तर
PQ is tangent to circle OM is perpendicular PQ chord AC and ∠COM = 65°
a. Here, ∠AOM = ∠COM = 65°
= 65° + 65°
= 130°
Now, ∠ABC = `1/2` ∠AOC ...(Since, angle at the centre is twice the angle formed by the same arc at any other point of the circle)
= `1/2 xx 130^circ`
= 65°
b. In ΔABC,
AB = AC
∠ABC = ∠ACB = 65° ...(Since, angles opposite to equal sides are equal)
∴ ∠BAC = 180° – (65° + 65°)
= 180° – 130°
= 50°
c. ∠OCQ = 90° ...(Since, angle between the radius and the tangent is 90°)
In ΔOMC,
∠OCM = 180° – (∠OMC + ∠MOC) ...[By angle sum property of triangle]
= 180° – (90° + 65°)
= 180° – 155°
= 25°
∠ACB = 65°
∠OCB = ∠ACB – ∠OCM
= 65° – 25°
= 40°
∠BCQ = ∠OCQ – ∠OCB
= 90° – 40°
= 50°
APPEARS IN
संबंधित प्रश्न
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB


In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
