Advertisements
Advertisements
प्रश्न
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
उत्तर
Given, AB is a diameter of the circle.
A tangent is drawn from point A.
Draw a chord CD parallel to the tangent MAN.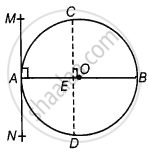
So, CD is a chord of the circle and OA is a radius of the circle.
∴ ∠MAO = 90° ...[Tangent at any point of a circle is perpendicular to the radius through the point of contact]
⇒ ∠CEO = ∠MAO ...[Corresponding angles]
∴ ∠CEO = 90°
Thus, OE bisects CD, ...[Perpendicular from centre of circle to chord bisects the chord]
Similarly, diameter AB bisects all chords which are parallel to the tangent at the point A.
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

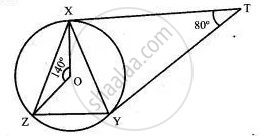
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
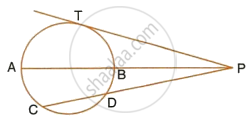
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
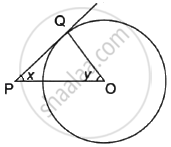
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
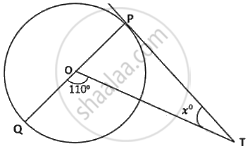
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.