Advertisements
Advertisements
प्रश्न
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
उत्तर
Steps of construction:
i) Draw a line segment OP = 6 cm
ii) With centre O and radius 3.5 cm, draw a circle
iii) Draw the midpoint of OP
iv) With centre M and diameter OP, draw a circle which intersect the circle at T and S
v) Join PT and PS.
PT and PS are the required tangents. On measuring the length of PT = PS = 4.8 cm

APPEARS IN
संबंधित प्रश्न
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (ii) radius of the circle.

If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

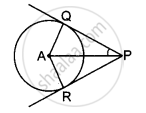
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

