Advertisements
Advertisements
प्रश्न
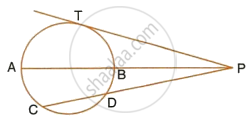
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
उत्तर
Given that,
CD = 7.8 cm, PD = 5 cm, PB = 4 cm
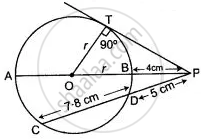
As we know,
PT2 = PD × PC
PT2 = PD × (PD + CD)
PT2 = 5 × 12.8
PT2 = 64
`=>` PT = 8 cm
Now in ΔPOT,
PO2 = OT2 + PT2
(r + 4)2 = r2 + 64
r2 + 16 + 8r = r2 + 64
8r = 48
r = 6
- Thus AB = 2r = 12 cm
- Length of tangent PT = 8 cm.
APPEARS IN
संबंधित प्रश्न
A circle can have ______ parallel tangents at the most.
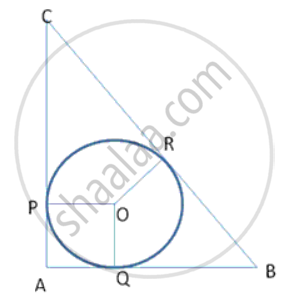
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
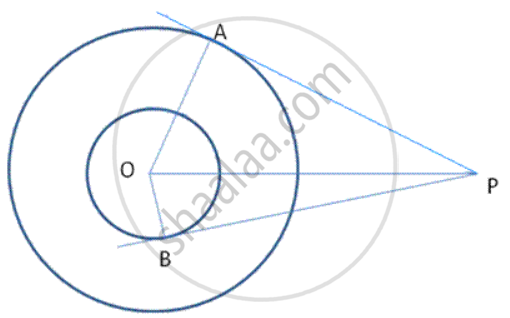
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
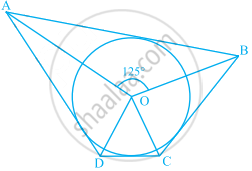
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
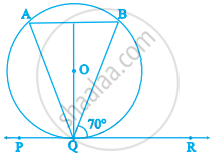
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

