Advertisements
Advertisements
प्रश्न
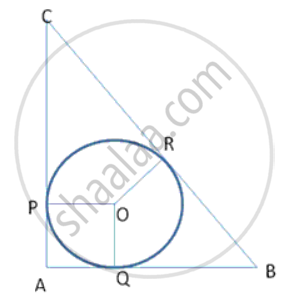
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
उत्तर
In right Δ BAC,
BC2= AC2+ AB2
AC2= 132 -52
AC2 = 169 - 25
AC2 = 144
AC = 12
Let OP = OQ = r (say) (radius of same circle)
∠ OQP = ∠ OPQ = 90° (radius is .L to tangent at the point of contact)
∴ OPAQ is a square.
AQ = AP = OP = OQ = r
BQ = BR = 5 - r ---(1) (length of tangents drawn from an external point)
PC = CR = 12 - r - (2) to a circle are equal}
BC = CR+ BR
13 = 12 - r + 5 - r [from (1) and {2}]
2r = 4
r = 2
Thus , radius of the circle is 2 cm
APPEARS IN
संबंधित प्रश्न
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.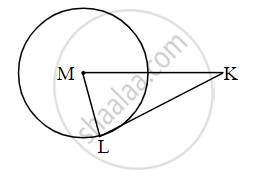
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
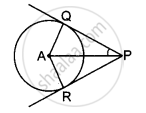
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

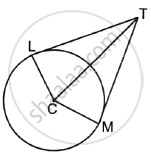
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.