Advertisements
Advertisements
प्रश्न
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
उत्तर
Let us first put the given data in the form of a diagram.
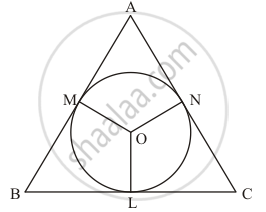
It is given that triangle ABC is isosceles with
AB = AC …… (1)
By looking at the figure we can rewrite the above equation as,
AM + MB = AN + NC
From the property of tangents we know that the length of two tangents drawn to a circle from the same external point will be equal. Therefore,
AM = AN
Let us substitute AN with AM in the equation (1). We get,
AM + MB = AM + NC
MB = NC …… (2)
From the property of tangents we know that the length of two tangents drawn from the same external point will be equal. Therefore we have,
MB = BL
NC = LC
But from equation (2), we have found that
MB = NC
Therefore,
BL = LC
Thus we have proved that point L bisects side BC.
APPEARS IN
संबंधित प्रश्न
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.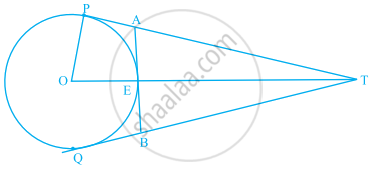
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
