Advertisements
Advertisements
प्रश्न
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
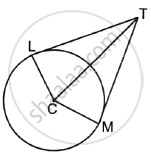
विकल्प
30°
60°
45°
55°
उत्तर
55°
Explanation:
In the given figure, TC bisects ∠LTM.
∴ ∠CTM = `1/2` ∠LTM
= `1/2` × 70°
= 35°
Also, ∠CMT = 90° ......[Tangent theorem]
In ΔTCM,
∠MCT + ∠CMT + ∠CTM = 180°
∠MCT + 90° + 35° = 180°
∠MCT = 180° – 90° – 35° = 55°
Thus, ∠MCT = 55°.
APPEARS IN
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is

In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
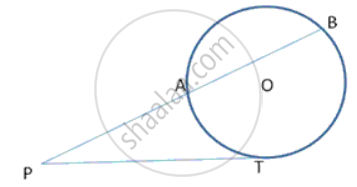
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
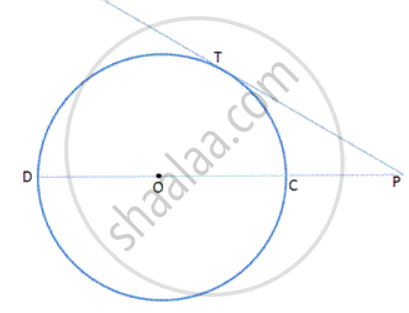
A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
Find the value of ∠DCE.

The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
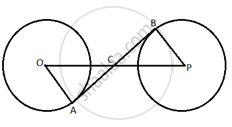
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

