Advertisements
Advertisements
प्रश्न
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

उत्तर

Given: Radius of the circle, r = 10 cm
Area of the circle = \[\pi \left( 10 \right)^2 = 3 . 14 \times 100 = 314 {cm}^2\]
\[ = \frac{1}{4} \times 314 \left[ From \left( 1 \right) \right]\]
\[ = 78 . 5 {cm}^2\]
\[ = \frac{1}{2} \times 10 \times 10\]
\[ = 50 {cm}^2\]
Area of the minor segment AQBP = Area of the sector OAPB − Area of the triangle BOA
= (78.5 − 50) cm2
= 28.5 cm2
= (314 − 28.5) cm2
= 285.5 cm2
APPEARS IN
संबंधित प्रश्न
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
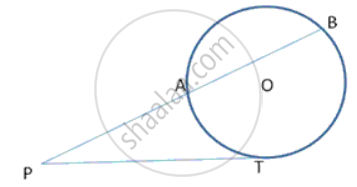
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

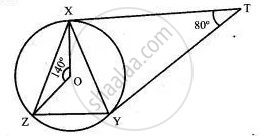
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
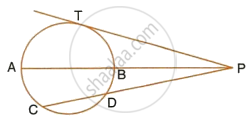
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
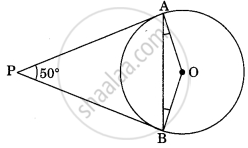
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______


In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
