Advertisements
Advertisements
Question
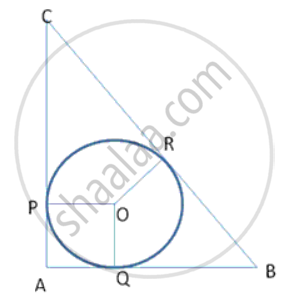
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
Solution
In right Δ BAC,
BC2= AC2+ AB2
AC2= 132 -52
AC2 = 169 - 25
AC2 = 144
AC = 12
Let OP = OQ = r (say) (radius of same circle)
∠ OQP = ∠ OPQ = 90° (radius is .L to tangent at the point of contact)
∴ OPAQ is a square.
AQ = AP = OP = OQ = r
BQ = BR = 5 - r ---(1) (length of tangents drawn from an external point)
PC = CR = 12 - r - (2) to a circle are equal}
BC = CR+ BR
13 = 12 - r + 5 - r [from (1) and {2}]
2r = 4
r = 2
Thus , radius of the circle is 2 cm
APPEARS IN
RELATED QUESTIONS
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
In Question 5 above, if radii of the two circles are equal, prove that AB = CD.
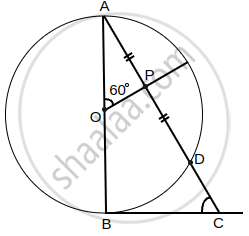
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.