Advertisements
Advertisements
प्रश्न
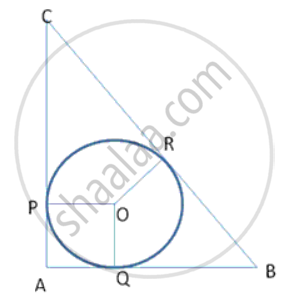
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
उत्तर
In right Δ BAC,
BC2= AC2+ AB2
AC2= 132 -52
AC2 = 169 - 25
AC2 = 144
AC = 12
Let OP = OQ = r (say) (radius of same circle)
∠ OQP = ∠ OPQ = 90° (radius is .L to tangent at the point of contact)
∴ OPAQ is a square.
AQ = AP = OP = OQ = r
BQ = BR = 5 - r ---(1) (length of tangents drawn from an external point)
PC = CR = 12 - r - (2) to a circle are equal}
BC = CR+ BR
13 = 12 - r + 5 - r [from (1) and {2}]
2r = 4
r = 2
Thus , radius of the circle is 2 cm
APPEARS IN
संबंधित प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

How many common tangents can be drawn to two circles, touching each
other externally?
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
