Advertisements
Advertisements
प्रश्न
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
पर्याय
Both Assertion (A) and Reason (R) are true and Reason (R) gives the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
उत्तर
Both Assertion (A) and Reason (R) are true but Reason (R) does not give the correct explanation of Assertion (A).
Explanation:
Assertion: A circle's tangent is always perpendicular to its radius through the point of contact.
Reason: Tangents drawn from an exterior point to a circle have the same length.
As a result, both reason and assertion are valid, but assertion is not the proper justification for reason.
APPEARS IN
संबंधित प्रश्न
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
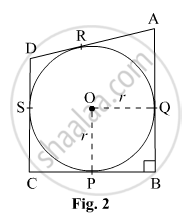
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
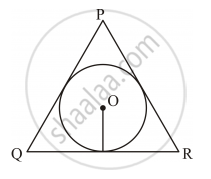
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
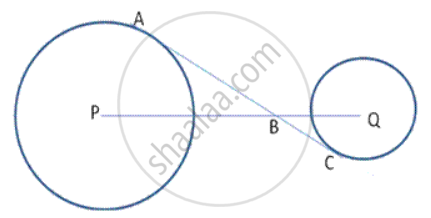
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
A circle of radius 5.2 cm has two tangents AB and CD parallel to each other. What is the distance between the two tangents?
