Advertisements
Advertisements
प्रश्न
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
उत्तर
Let PQ and PR touch the circle at points S and U respectively. Join O with P, Q, R, S and U.
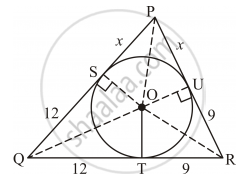
We have, OS = OT = OU = 6 cm (Radii of the circle)
QT = 12 cm and TR = 9 cm
∴ QR = QT + TR = 12 cm + 9 cm = 21 cm
Now, QT = QS = 12 cm (Tangents from the same point)
TR = RU = 9 cm
Let PS = PU = x cm
Then, PQ = PS + SQ = (12 + x) cm and PR = PU + RU = (9 + x) cm
It is clear that
ar (ΔOQR) + ar (ΔOPR) + ar (ΔOPQ) = ar (ΔPQR)
`rArr 1/2xxQRxxOT+1/2xxPRxxOU+1/2xxPQxxOS=189` `(given : ar(Δ PQR)=189cm^2)`
`rArr 1/2xx21xx6+1/2xx(9+x)xx6+1/2xx(12+x)xx6=189`
`rArr 1/2xx6(21+9+x+12+x)=189`
⇒ 3 (42 + 2x) = 189
⇒ 42 + 2x = 63
⇒ 2x = 21
⇒ x = 10.5
Thus, PQ = (12 + 10.5) cm = 22.5 cm and PR = (9 + 10.5) cm = 19.5 cm.
APPEARS IN
संबंधित प्रश्न
The common point of a tangent to a circle and the circle is called ______.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
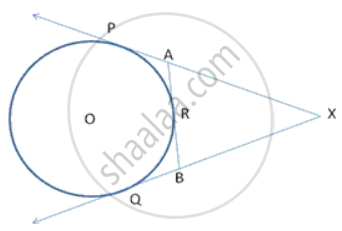
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
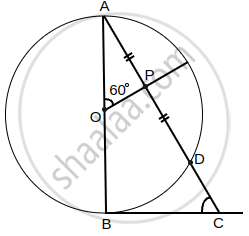
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
