Advertisements
Advertisements
प्रश्न
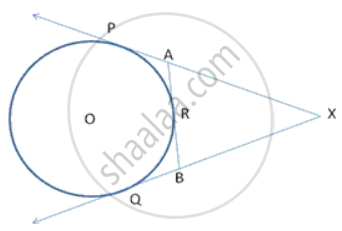
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
उत्तर
XP = XQ
AR = AP
BR = BQ {Length of tangents drawn from an external point to a circle are equal}
XP = XQ
XA + AP = XB + BR
XA + AR = XB + BR {Using {1)}
APPEARS IN
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

A point A is 17cm from the centre of the circle. The length of the tangent drawn from A to the circle is 15cm. find the radius of the circle.
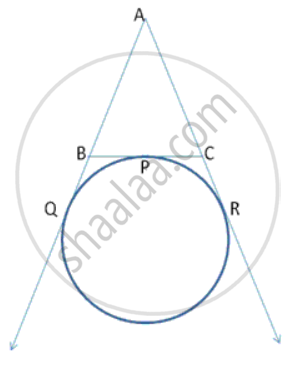
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
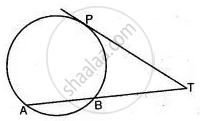
In the figure given below, PT is a tangent to the circle. Find PT if AT = 16 cm and AB = 12 cm.
Tangents from an external point to a circle are ______
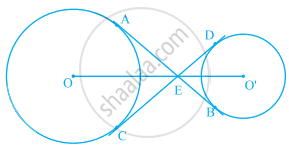
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
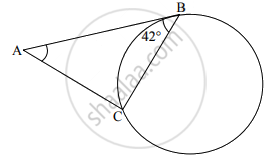
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
