Advertisements
Advertisements
प्रश्न
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
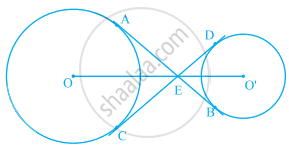
The common tangents AB and CD to two circles with centres O and O' intersect at E between their centres. Prove that the points O, E and O' are collinear.
उत्तर
Join AO, OC and O’D, O’B.
Now, in ∆EO’D and ∆EO’B,
O’D = O’B
O’E = O’E
ED = EB ...[Tangents drawn from an external point to the circle are equal in length]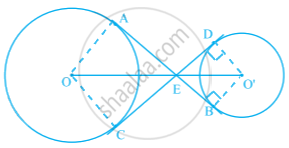
∴ EO’D ≅ ∆ EO’B ...[By SSS congruence criterion]
⇒ ∠O’ED = ∠O’EB ...(i)
i.e., O’E is the angle bisector of ∠DEB.
Similarly, OE is the angle bisector of ∠AEC.
Now, in quadrilateral DEBO’.
∠O’DE = ∠O’BE = 90° ...[CED is a tangent to the circle and O’D is the radius, i.e., O’D ⊥ CED]
⇒ ∠O’DE + ∠O’BE = 180°
∴ ∠DEB + ∠DO’B = 180° ...(ii) [∵ DEBO’ is cyclic quadrilateral]
Since, AB is a straight line.
∴ ∠AED + ∠DEB = 180°
⇒ ∠AED + 180° – ∠DO’B = 180° ...[From (ii)]
⇒ ∠AED = ∠DO’B ...(iii)
Similarly, ∠AED = ∠AOC ...(iv)
Again from equation (ii),
∠DEB = 180° – ∠DO’B
Dividing by 2 on both sides, we get
`1/2 ∠"DEB" = 90^circ - 1/2 ∠"DO'B"`
⇒ ∠DE'O = 90° `-1/2` ∠DO'B ...(v) [∵ O'E is the angle bisector of ∠DEB i.e. `1/2` ∠DEB = ∠DEO']
Similarly, ∠AEC = 180° – ∠AOC
Dividing by 2 on both sides, we get
`1/2 ∠"AEC" = 90^circ - 1/2 ∠"AOC"`
⇒ `∠"AEO" = 90^circ - 1/2 ∠"AOC"` ...(vi) [∵ OE is the angle bisector of ∠AEC i.e., `1/2 ∠"AEC" = ∠"AEO"`]
Now, ∠AED + ∠DEO' + ∠AEO = ∠AED + `(90^circ - 1/2 ∠"DO'B") + (90^circ - 1/2 ∠"AOC")`
= `∠"AED" + 180^circ - 1/2 (∠"DO'B" + ∠"AOC")`
= `∠"AED" + 180^circ - 1/2 (∠"AED" + ∠"AED")` ...[From equation (iii) and (iv)]
= `∠"AED" + 180^circ - 1/2 (2 xx ∠"AED")`
= ∠AED + 180° – ∠AED = 180°
∴ ∠AED + ∠DEO' + ∠AEO = 180°
So, OEO’ is straight line.
Hence, O, E and O’ are collinear.
संबंधित प्रश्न
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

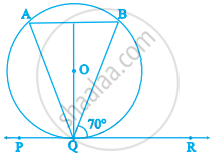
In figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to ______.
The distance between two parallel tangents of a circle of radius 4 cm is ______
In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.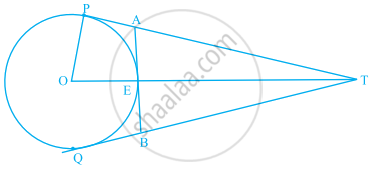
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

How many tangents can be drawn to a circle from a point on it?
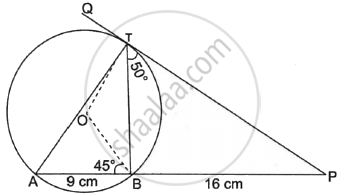
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT