Advertisements
Advertisements
प्रश्न
How many tangents can be drawn to a circle from a point on it?
पर्याय
One
Two
Infinite
Zero
उत्तर
One
Explanation:
We are aware that only one tangent can be drawn from a point to a circle.
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
In following fig., ABC is a right- angled triangle at A with sides AB = 5 cm and BC = 13 cm . A circle with centre O has been inscribed in the triangle ABC. Calculate the radius of the incircle.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
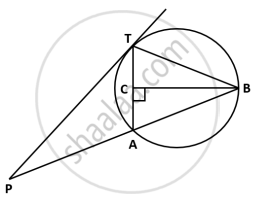

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
