Advertisements
Advertisements
प्रश्न
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
उत्तर
We shall prove that ∠ACP = ∠BCP = 90°
and AC = BC
Now, ∠APC = ∠BPC
Since O lies on the bisector of ∠APB.
Δs ACP and BCP are congruent triangles by SAS congruence criterion,
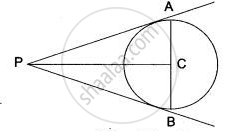
∴ AC = BC
and ∠ ACP = ∠ BCP
Since ∠ ACP + ∠ BCP = 180°
2 ∠ ACP = 180°
∠ ACP = 90°
∠ACP = ∠BCP = 90°
Hence proved.
APPEARS IN
संबंधित प्रश्न
A tangent to a circle intersects it in ______ point (s).
The common point of a tangent to a circle and the circle is called ______.
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
