Advertisements
Advertisements
प्रश्न
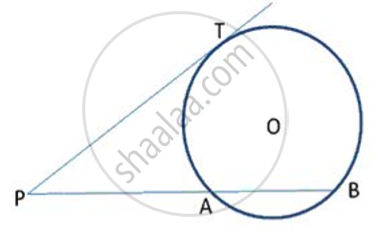
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
उत्तर
Let PT = x cm
Since, PAB is a secant and PT is a tangent to the given circle, we have,
PA · PB = PT2
⇒ 4.9 = PT2
⇒ PT2 = 36
⇒ PT = 6 cm
APPEARS IN
संबंधित प्रश्न
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
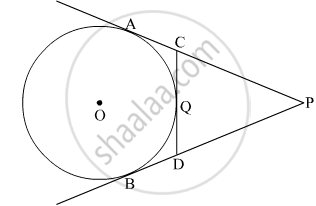
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = Scm, find PT.
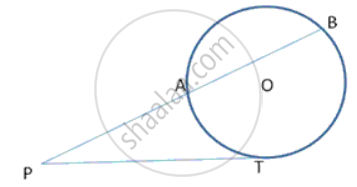
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB


In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
