Advertisements
Advertisements
प्रश्न
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

उत्तर
In the given figure,
\[ \Rightarrow \angle AOC = 180^o - 130^o = 50^o\]
\[ \Rightarrow \angle AOC = 180^0- 130^o = 50^0\] (Because the tangent at any point of a circle is perpendicular to the radius through the point of contact)
\[\angle AOC + \angle CAO + \angle ACO = 180^o \left( \text{Angle sum property of a triangle} \right)\]
\[\angle AOC + \angle CAO + \angle ACO = 180^o\left( \text{Angle sum property of a triangle} \right)\]
APPEARS IN
संबंधित प्रश्न
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
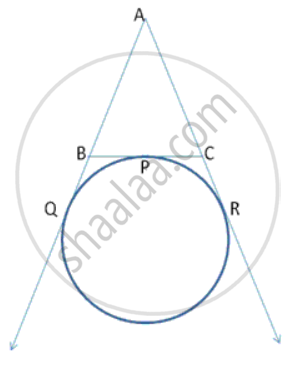
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

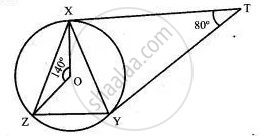
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
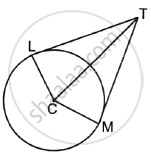
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

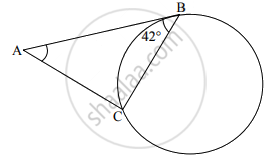
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
