Advertisements
Advertisements
प्रश्न
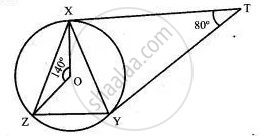
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
उत्तर
∠ TXY = ∠ TYX = 50° ...(since XT = YT)
∠ OXZ = ∠ OZX = 20° ...(since OX = OZ)( In ΔXOZ, 140° + ∠ OXZ + ∠OZX = 180°)
⇒ ∠ OXZ = 20°
⇒ ∠ OXY = 40° ...(Since ∠OXT = 90°)
⇒ ∠ZXY = ∠ OXZ + ∠ OXY
= 20° + 40° = 60°.
APPEARS IN
संबंधित प्रश्न
A line intersecting a circle in two points is called a ______.
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
How many common tangents can be drawn to two circles, touching each
other externally?
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
PA and PB are tangents from P to the circle with centre O. At M, a tangent is drawn cutting PA at K and PB at N. Prove that KN = AK + BN.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.


In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
