Advertisements
Advertisements
प्रश्न

In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is ______.
पर्याय
4.2 cm
2.1 cm
8.4 cm
6.3 cm
उत्तर
In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is 8.4 cm.
Explanation:
The figure shows two circles touching externally at point A, with QR being a common tangent. The tangent at A meets QR at point P, and we are given that the length AP = 4.2 cm. To find the length of QR, we can use the fact that the tangents drawn from an external point to a circle are equal in length.
Since A is the point of tangency for both circles, the lengths of the tangents from P to each point of tangency (which are Q and R respectively) will be equal. Thus, PQ = PR = AP.
Given AP = 4.2 cm, we can say PQ = PR = 4.2 cm.
Therefore, the length of QR,
QR = PQ + PR
QR = 4.2 + 4.2
QR = 8.4 cm
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

In the given circle with centre O, ∠ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.

In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
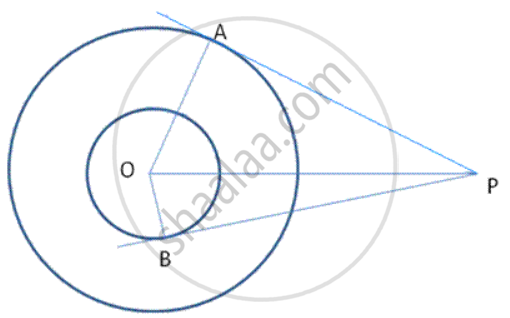
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
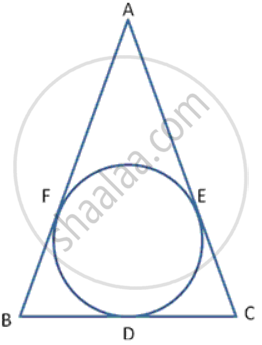
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Find the value of ∠DCE.

In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
