Advertisements
Advertisements
प्रश्न
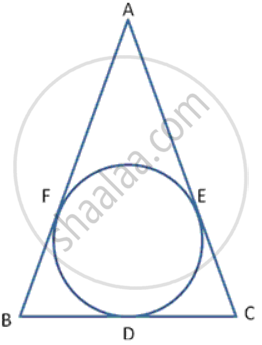
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
उत्तर
To prove:- AF + BD + CE = AE + BF + CD
Proof:- AF = AE ----(1) {Length of tangents drawn from an external point to a circle are equal }
BD = BF ----(2}
CE = CD ----(3}
Adding (1), {2} and {3}
AF + BD + CE = AE + BF + CD
APPEARS IN
संबंधित प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
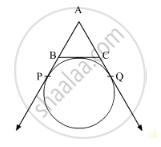
In Figure 1, AP, AQ and BC are tangents to the circle. If AB = 5 cm, AC = 6 cm and BC
= 4 cm, then the length of AP (in cm) is
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
In following fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PA = 4cm and AB = Scm, find PT.
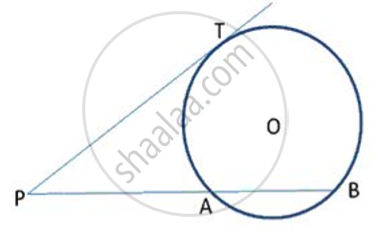
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

Tangents from an external point to a circle are ______
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

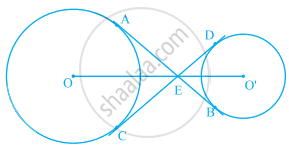
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.
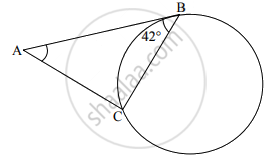
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
