Advertisements
Advertisements
प्रश्न
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

उत्तर

m∠OPT 90º (radius is perpendicular to the tangent)
So, ∠OPQ = ∠OPT - ∠QPT
= 90º - 60º
= 30º
m∠POQ = 2m∠QPT = 2 x 60º = 120º
reflex m∠POQ = 360º - 120º= 240º
`/_PQR=1/2 "reflex"/_POQ`
`=1/2 xx 240^@`
`=120^@`
`m/_PRQ=120^@`
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

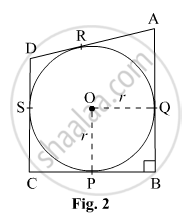
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
In Fig. the incircle of ΔABC touches the sides BC, CA, and AB at D, E respectively. Show that: AF + BD + CE = AE + BF + CD = `1/2`( Perimeter of ΔABC)

Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
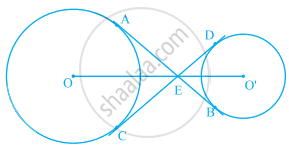
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.