Advertisements
Advertisements
प्रश्न
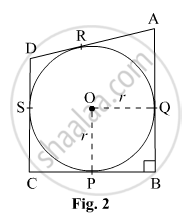
In Fig.2, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches the sides BC, AB, AD and CD at points P, Q, R and S respectively, If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm.) is:
पर्याय
(A) 11
(B) 18
(C) 6
(D) 15
उत्तर
We know that, the lengths of the tangents drawn from an external point to a circle are equal.
DS = DR = 5 cm
∴ AR = AD − DR = 23 cm − 5 cm = 18 cm
AQ = AR = 18 cm
∴ QB = AB − AQ = 29 cm − 18 cm = 11 cm
QB = BP = 11 cm
In right Δ PQB, PQ2 = QB2 + BP2 = (11 cm)2 + (11 cm)2 = 2 × (11 cm)2
PQ = `11sqrt2r` cm … (1)
In right ΔOPQ,
PQ2 = OQ2 + OP2 = r2 + r2 = 2 r2
PQ = `11sqrt2r`… (2)
From (1) and (2), we get
r = 11 cm
Thus, the radius of the circle is 11 cm.
APPEARS IN
संबंधित प्रश्न
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
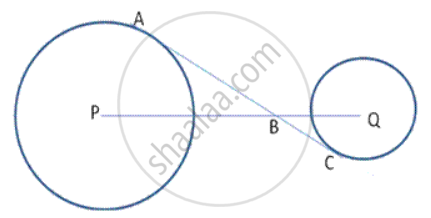
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle APB

If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
In the given figure, AB is diameter of a circle centered at O. BC is tangent to the circle at B. If OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
ΔABC circumscribes a circle of radius r such that ∠B = 90°. If AB = 3 cm and BC = 4 cm, then find the value of r.
