Advertisements
Advertisements
प्रश्न
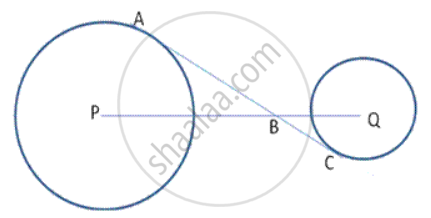
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
उत्तर
To find :- PQ
Let BC= x cm
∴ AC= 8 + x
By Pythagcras theorem BQ = `sqrt ("x"^2 + 9)`
AC2 = PQ2 -92
`=> (8 + "x")^2 = (10 + sqrt ("x"^2 + 9))^2 - 81`
`=> 64 + "x"^2 + 16"x" = 100 + "x"^2 + 9 + 20 sqrt ("x"^2 + 9)`
`=> 5 sqrt ("x"^2 + 9) = 9 + 4"x"`
Squaring both sides
⇒ 25(x2 + 9) = 81 + l6x2 + 72x
⇒ 9x2 - 72x - 144 = 0
⇒ x2 - 8x - 16 = 0
(x - 4)2 = 0
⇒ x = 4
BQ = `sqrt (4^2 + 9) = sqrt 25 = 5`
⇒ PQ = PB + BQ
⇒ PQ = 10 + 5
⇒ PQ = 15 cm
APPEARS IN
संबंधित प्रश्न
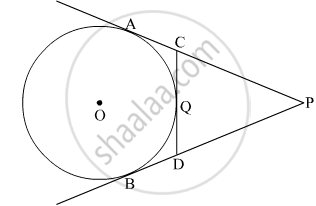
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
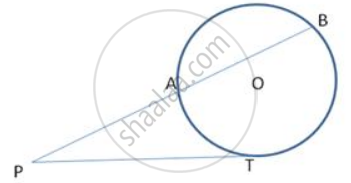
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
The tangents drawn at the extremities of the diameter of a circle are ______.
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

How many tangents can be drawn to a circle from a point on it?
