Advertisements
Advertisements
प्रश्न
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
उत्तर
ABCD is a quadrilateral. Suppose a circle touches the sides AB, BC, CD and DA of the quadrilateral ABCD at P, Q, R and S, respectively.
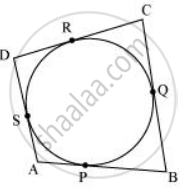
We know that the length of tangents drawn from an external point to a circle are equal.
DR = DS ...(1)
CR = CQ ...(2)
BP = BQ ...(3)
AP = AS ...(4)
Adding (1), (2), (3) and (4), we get
DR + CR + BP + AP = DS + CQ + BQ + AS
(DR + CR) + (BP + AP) = (DS + AS) + (CQ + BQ)
CD + AB = AD + BC
Or, AB + CD = BC + DA
APPEARS IN
संबंधित प्रश्न
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 

In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
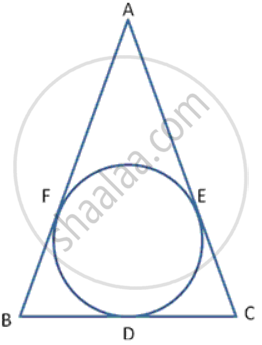
If Δ PQR is isosceles with PQ = PR and a circle with centre O and radius r is the incircle of the Δ PQR touching QR at T, prove that the point T bisects QR.
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find:
- AB.
- the length of tangent PT.
A tangent JK is drawn to a circle with centre C such that CK = 6 cm and ∠CKJ = 60°. Find the length of the tangent JK.

In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

