Advertisements
Advertisements
प्रश्न
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
पर्याय
4 cm
5 cm
6 cm
8 cm
उत्तर
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is 8 cm.
Explanation:
First, draw a circle of radius 5 cm with centre O.
A tangent XY is drawn at point A.
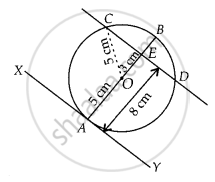
A chord CD is drawn which is parallel to XY and at a distance of 8 cm from A.
Now, ∠OAY = 90° ...[∵ Tangent at any point of circle is perpendicular to the radius through the point of contact]
∠OAY + ∠OED = 180° ...[∵ Sum of cointerior angles is 180°]
⇒ ∠OED = 180° – 90° = 90°
Also, AE = 8 cm.
Join OC
OC = 5 cm ...[Radius of circle]
OE = AE – OA
= 8 – 5
= 3 cm
Now, in right angled ∆OEC,
OC2 = OE2 + EC2 ...[By Pythagoras theorem]
⇒ EC2 = OC2 – OE2
⇒ EC2 = 52 – 32
⇒ EC2 = 25 – 9 = 16
⇒ EC = 4 cm
Since, perpendicular from centre to the chord bisects the chord.
∴ CE = ED
⇒ CD = 2 × EC
⇒ CD = 2 × 4
⇒ CD = 8 cm
APPEARS IN
संबंधित प्रश्न
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate ∠ PAD.

In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
Tangents from an external point to a circle are ______
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?
The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Assertion (A): A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R): The lengths of tangents drawn from an external point to a circle are equal.
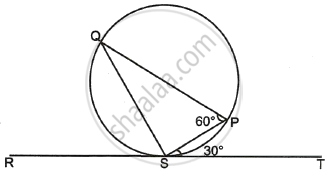
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.