Advertisements
Advertisements
प्रश्न
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

उत्तर
In ΔAPO, ∠AOC is the exterior angle
∴ From exterior angle property.
∠AOC = ∠PAO + ∠APB ...`{{:(∵ ∠AOC = 130^circ ("Given")),(∠PAO = 90^circ "(radius and tangent"),("are" ⊥ "to each other at the point of contact)"):}`
`\implies` 130° = 90° + ∠APB
`\implies` ∠APB = 130° – 90°
`\implies` ∠APB = 40°
संबंधित प्रश्न
A line intersecting a circle in two points is called a ______.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
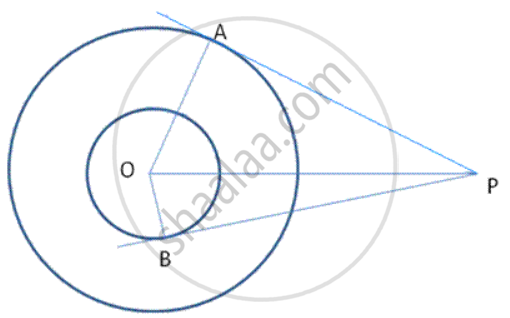
In followinf fig., two concentric circles with centre 0 are of radii 5 cm and 3 cm. from an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.
Tangents from an external point to a circle are ______
A: What is a line called, if it meets the circle at only one point?
B: Collection of all points equidistant from a fixed point is ______.
- Chord
- Tangent
- Circle
- Curve
- Secant
Which is correct matching?

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
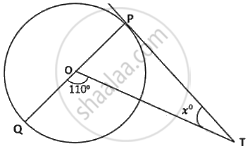
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.