Question

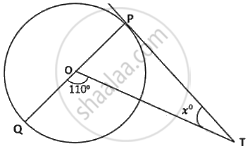
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.

पर्याय

• 20°

• 40°

• 55°

• 70°

Answer 1

In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is 20°.

Explanation:

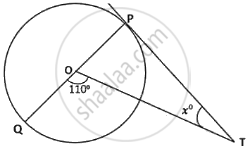
Given:

• O is the center of the circle.
• PT is a tangent to the circle at point T.

When a tangent and a radius intersect at the point of tangency, the angle formed between the radius and the tangent is 90°. This is a key property of circles and tangents.

Let's analyze the situation step by step:

Step-by-Step Solution

1. Identify the key points and angles:

• O is the center.
• PT is the tangent.
• OT is the radius.
• ∠OTP = 90° because the radius and tangent are perpendicular at the point of tangency.

2. Determine the relationship involving z:

Suppose we have a triangle OTP, where T is the point of tangency. Let's consider an angle ∠OTP which is 90°, and we are given that x = 20°.

3. Use the properties of the right triangle:

Since ∠OTP = 90°, we can identify other angles in the triangle.

If there is another angle related to a in this problem, let's denote it as ∠TOP.

Assuming x is a part of the complementary angle

Let's assume x is related to ∠OTP.

• ∠OTP + ∠PTO + ∠TOP = 180°   ...(Sum of angles in a triangle)
• Given ∠OTP = 90°, we have:
  90° + ∠PTO + x = 180°
• Simplifying:
  ∠PTO + x = 90°
• Given x = 20°:
  ∠PTO + 20° = 90°
  ∠PTO + 70°

So, the given value x = 20° complements ∠PTO which results in a 70° angle to satisfy the conditions of the right triangle formed by the tangent and radius.