Advertisements
Advertisements
Question
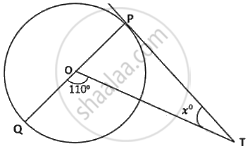
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.
Options
20°
40°
55°
70°
Solution
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is 20°.
Explanation:
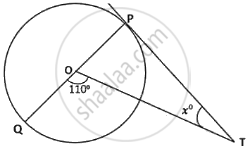
Given:
- O is the center of the circle.
- PT is a tangent to the circle at point T.
When a tangent and a radius intersect at the point of tangency, the angle formed between the radius and the tangent is 90°. This is a key property of circles and tangents.
Let's analyze the situation step by step:
Step-by-Step Solution
1. Identify the key points and angles:
- O is the center.
- PT is the tangent.
- OT is the radius.
- ∠OTP = 90° because the radius and tangent are perpendicular at the point of tangency.
2. Determine the relationship involving z:
Suppose we have a triangle OTP, where T is the point of tangency. Let's consider an angle ∠OTP which is 90°, and we are given that x = 20°.
3. Use the properties of the right triangle:
Since ∠OTP = 90°, we can identify other angles in the triangle.
If there is another angle related to a in this problem, let's denote it as ∠TOP.
Assuming x is a part of the complementary angle
Let's assume x is related to ∠OTP.
- ∠OTP + ∠PTO + ∠TOP = 180° ...(Sum of angles in a triangle)
- Given ∠OTP = 90°, we have:
90° + ∠PTO + x = 180° - Simplifying:
∠PTO + x = 90° - Given x = 20°:
∠PTO + 20° = 90°
∠PTO + 70°
So, the given value x = 20° complements ∠PTO which results in a 70° angle to satisfy the conditions of the right triangle formed by the tangent and radius.
APPEARS IN
RELATED QUESTIONS
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
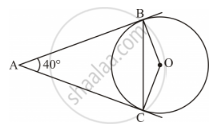
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is ______
In figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to ______.

In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

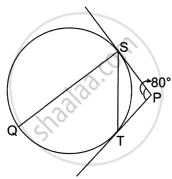
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.