Advertisements
Advertisements
Question
From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
Options
A. 25
B. `sqrt313`
C. 5
D. 1
Solution
The given information can be represented diagrammatically as follows:

Let O be the centre of the circle.
Given: PQ = 12 cm and OQ = 13 cm.
To find: Radius of the circle
PQ is a tangent drawn from the external point Q to the circle.
∠ OPQ = 90° (Radius is perpendicular to the tangent at the point of contact)
On applying Pythagoras theorem in ΔOPQ, we obtain:
OQ2 = OP2 + PQ2
∴ OP2 = OQ2 − PQ2
⇒ OP2 = (13 cm)2 − (12 cm)2
⇒ OP2 = 169cm2 − 144 cm2
⇒ OP2 = 25 cm2
⇒ OP = 5 cm
Thus, the radius of circle is 5 cm.
Hence, the correct answer is C
APPEARS IN
RELATED QUESTIONS
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
The given figure shows a circle with centre O and BCD is tangent to it at C. Show that : ∠ACD + ∠BAC = 90°.

In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

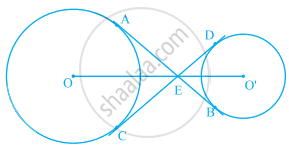
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
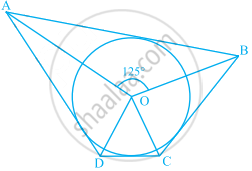
In figure, the common tangent, AB and CD to two circles with centres O and O' intersect at E. Prove that the points O, E, O' are collinear.