Advertisements
Advertisements
Question
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

Solution
Given: A circle with center P. CB tangent and line AC intersect a circle in point D
Construction: Join BD.
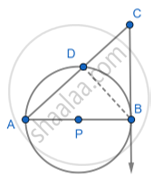
To Prove: ∴ ∠ADB =90° [Angle inscribed in semicircle]
∴ ∠PBC = 90° [Tangent perpendicular to the radius]
i.e. ∠ABC =90°
In Δ ACB and Δ ABD
∠ ABC = ∠ ADB [Each is of 90°]
∴ ∠ CAB = ∠DAB [Common angle]
∴ ΔACB ∼ ΔABD [AA property]
∴ `"AC"/"AB"="AB"/"AD"`
∴AC × AD = (AB)2…(1)
AP = PB …(radii of the same circle)
∴ AB = AP +PB
∴ AB = 2AP
Substituting the value of AB in equation (1)
AC × AD = (2AP)2
∴ AC × AD = 4(AP)2
∴ AC × AD =4 (radius)2
APPEARS IN
RELATED QUESTIONS
The common point of a tangent to a circle and the circle is called ______.
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
What is the distance between two parallel tangents of a circle having radius 4.5 cm ? Justify your answer.
Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
The tangents drawn at the extremities of the diameter of a circle are ______.
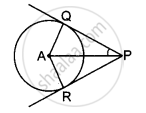
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______

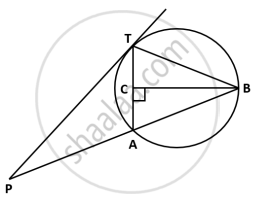
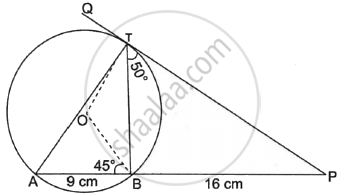
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
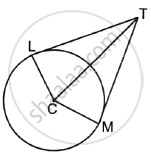
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
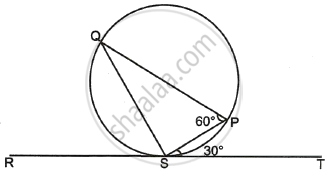
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.
In the given figure O, is the centre of the circle. CE is a tangent to the circle at A. If ∠ABD = 26° find:
- ∠BDA
- ∠BAD
- ∠CAD
- ∠ODB

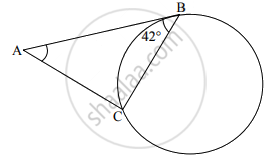
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
