Advertisements
Advertisements
Question
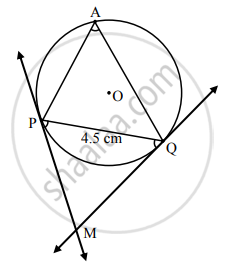
Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
Solution
Rough Figure:
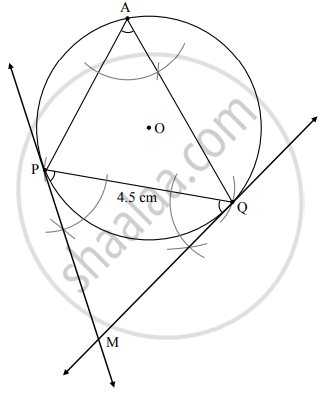
Steps of construction:
- Draw a circle of radius 2.7 cm.
- Draw a chord PQ of length 4.5 cm.
- Take a point A on the major arc, other than P and Q.
- Join PA and QA.
- Using P and Q as vertices and chord PQ as one side, draw ∠MPQ and ∠MQP equal to ∠PAQ.
- Lines containing the rays PM and QM are the tangents to the circle at P and Q respectively.
APPEARS IN
RELATED QUESTIONS
In Fig. 1, PQ is a tangent at a point C to a circle with centre O. if AB is a diameter and ∠CAB = 30°, find ∠PCA.

A circle can have ______ parallel tangents at the most.
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

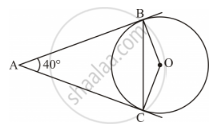
In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______

In the figure, point Q is the
point of contact. If PQ = 12,
PR = 8 then find PS.
A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisects the arc PRQ.
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
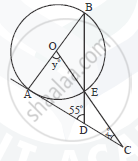
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
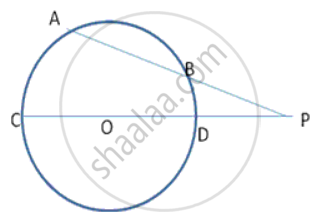
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
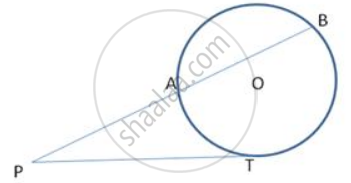
Calculate the length of direct common tangent to two circles of radii 3cm and Bern with their centres 13cm apart.
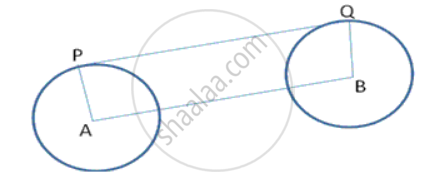
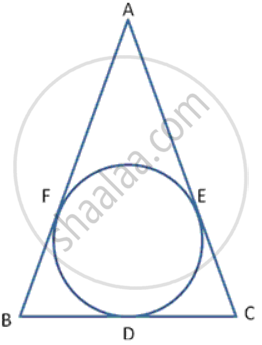
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ∠ BAM = ∠ BMA
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Find the value of ∠DCE.

In figure, O is the centre of a circle of radius 5 cm, T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB.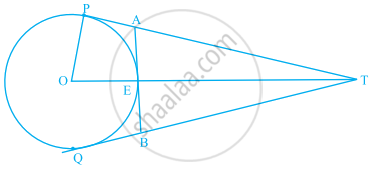
Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

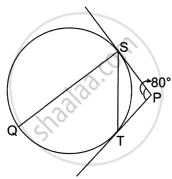
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.