Advertisements
Advertisements
Question

In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
Solution
Proof: From figure

Seg AB ⊥ seg BC and seg AD ⊥ seg CD .......[By tangent theorem]
∴ ∠ABC = ∠ADC = 90°
In □ABCD,
∠A + ∠B + ∠C + ∠D = 360° ......[Angle of the square]
∴ ∠A + 90° + ∠C + 90° = 360°
∴ ∠A + ∠C = 360° – 180°
∴ ∠A + ∠C = 180°
∴ ∠A + m(arc BXD) = 180° [Central angle] ......(i)
Now, m(arc BXD) + m(arc BYD) = 360° ......[Two arcs contribute a complete circle] ......(ii)
Now, multiply equation (i) by 2 on both sides
2[∠A + m(arc BXD)] = 2 × 180°
∴ 2∠A + 2 × m(arc BXD) = 360°
∴ 2∠A = 360 – 2 × m(arc BXD)
∴ 2∠A = m(arc BXD) + m(arc BYD) – 2m(arc BXD)
∴ 2∠A = m(arc BYD) – m(arc BXD) .....[From (ii)]
∴ ∠A = `1/2` [m(arc BYD) – m(arc BXD)]
Hence proved.
APPEARS IN
RELATED QUESTIONS
A tangent to a circle intersects it in ______ point (s).
In the given figure O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm. Calculate the radius of a circle.

In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
In fig. 5 is a chord AB of a circle, with centre O and radius 10 cm, that subtends a right angle at the centre of the circle. Find the area of the minor segment AQBP. Hence find the area of major segment ALBQA. (use π = 3.14)

From a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
In Figure 5, a triangle PQR is drawn to circumscribe a circle of radius 6 cm such that the segments QT and TR into which QR is divided by the point of contact T, are of lengths 12 cm and 9 cm respectively. If the area of ΔPQR = 189 cm2, then find the lengths of sides PQ and PR.
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
Two chords AB and CD of lengths 6cm and 12cm are drawn parallel inside the circle. If the distance between the chords of the circle is 3cm, find the radius of the circle.
In fig., AB and DC are two chords of a circle with centre O. these chords when produced meet at P. if PB = Bern, BA = 7cm and PO = 14.5cm, find the radius of the circle.
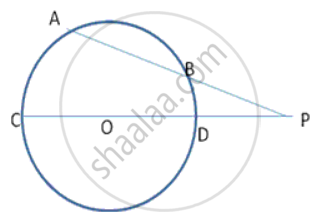
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
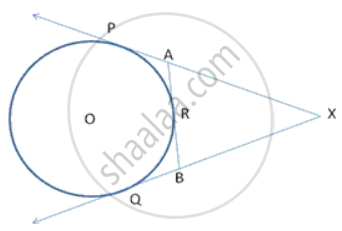
In the figure, XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that XA + AR = XB + BR.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.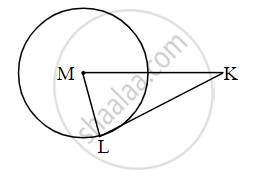
Find the value of ∠DCE.

Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is ______.
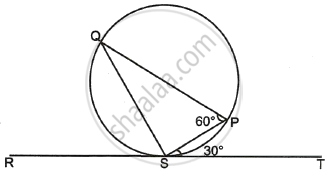
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.