Advertisements
Advertisements
Question
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.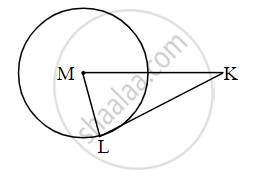
Solution
(i)
Line KL is the tangent to the circle at point L and seg ML is the radius. ......[Given]
∴ ∠MLK = 90° ......(i) [Tangent theorem]
In ∆MLK,
∠MLK = 90°
∴ MK2 = ML2 + KL2 .....[Pythagoras theorem]
∴ 122 = ML2 + `(6sqrt(3))^2`
∴ 144 = ML2 + 108
∴ ML2 = 144 − 108
∴ ML2 = 36
∴ ML = `sqrt(36)`
∴ ML = 6 units ......[Taking square root of both sides]
∴ Radius of the circle is 6 units.
(ii)
We know that,
ML = `1/2` MK,
∴ ∠K = 30° .....(ii) [Converse of 30°−60°−90° theorem]
In ∆MLK,
∠L = 90° .....[From (i)]
∠K = 30° .....[From (ii)]
∴ ∠M = 60° ......[Remaining angle of ∆MLK]
APPEARS IN
RELATED QUESTIONS
A circle can have ______ parallel tangents at the most.
Draw a circle of radius 3.5 cm. Marks a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent.
In the adjoining figure the radius of a circle with centre C is 6 cm, line AB is a tangent at A. Answer the following questions.
(1) What is the measure of ∠CAB ? Why ?
(2) What is the distance of point C from line AB? Why ?
(3) d(A,B) = 6 cm, find d(B,C).
(4) What is the measure of ∠ABC ? Why ? 
Draw Δ ABC such that, AB = 8 cm, BC = 6 cm and ∠ B = 90°. Draw seg BD
perpendicular to hypotenuse AC. Draw a circle passing through points
B, D, A. Show that line CB is a tangent of the circle.
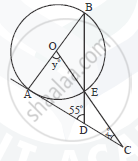
In the given figure AC is a tangent to the circle with centre O.
If ∠ADB = 55° , find x and y. Give reasons for your answers.
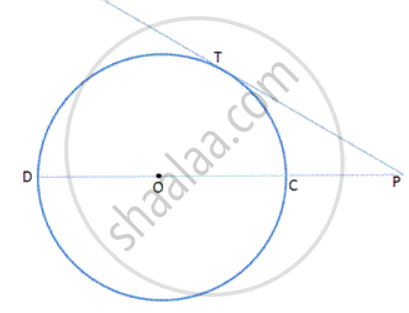
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
The length of the direct common tangent to two circles of radii 12cm and 4cm is 15cm. calculate the distance between their centres.
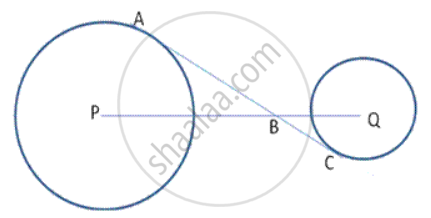
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
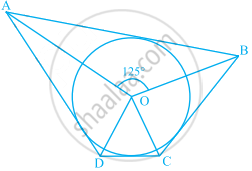
In figure, if ∠AOB = 125°, then ∠COD is equal to ______.
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

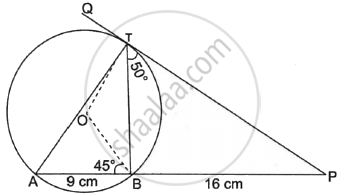
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
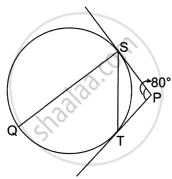
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.