Advertisements
Advertisements
Question
Construct a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution

Steps of construction:
- Draw a circle with a radius of 5 cm with the centre as O.
- Take point A on the circumference of the circle and join OA.
- Draw a radius OB, making an angle of 120° (180° – 60°) with OA.
- Draw a perpendicular to OB at point B and a perpendicular to OA at point A. Let both perpendiculars intersect at point P.
- PA and PB are the required tangents at an angle of 60°.
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
The common point of a tangent to a circle and the circle is called ______.
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
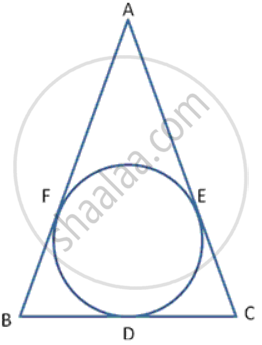
In following figure , the incircle of Δ ABC , touches the sides BC , CA and AB at D , E and F respectively. Show AF + BD + CE = AE + BF + CD
Find the area of sector whose central angle and radius are 60o and 21 cm respectively.
`(pi = 22/7)`
In the following figure, seg AB is the diameter of the circle with center P. Line CB be the tangent and line AC intersects a circle in point D. Prove that:
AC x AD = 4 (radius)2

The quadrilateral formed by joining the angle bisectors of a cyclic quadrilateral is a ______
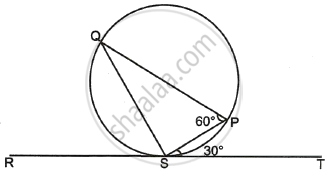
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.
In the given diagram an isosceles ΔABC is inscribed in a circle with centre O. PQ is a tangent to the circle at C. OM is perpendicular to chord AC and ∠COM = 65°.

Find:
- ∠ABC
- ∠BAC
- ∠BCQ
