Advertisements
Advertisements
Question
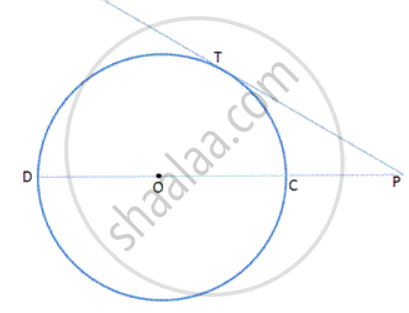
In following fig., PT is tangent to the circle at T and CD is a diameter of the same circle. If PC= 3cm and PT= 6cm, find the radius of the circle.
Solution
Let OD = OC = x cm (radius of same circle)
Since, PCD is a secant and PT is a tangent to the given circle, we have
PC · PD = PT2
3 . (3 +2x) = 62
⇒ 9 + 6x = 36
⇒ 6x = 27
⇒ x = `27/6 = 9/2`
Radius of the circle is `9/2` cm , diameter is 9 cm
APPEARS IN
RELATED QUESTIONS
Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
In Fig. 1, AOB is a diameter of a circle with centre O and AC is a tangent to the circle at A. If ∠BOC = 130°, the find ∠ACO.

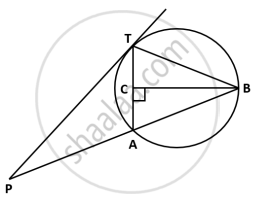
In fig., PT is a tangent to the circle at T and PAB is a secant to the same circle. If PB = 9cm and AB = 5 cm, find PT.
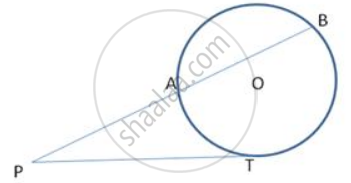
Find the length of the tangent from a point which is at a distance of 5cm from the centre of the circle of radius 3cm.
In the following figure, seg AB is a diameter of the circle, m (arc AKC) = 40°. Find the value of m (arc BMC).
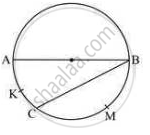
Prove that the tangents drawn at the ends of a chord of a circle make equal angles with the chord.
In the given figure, PT is a tangent to the circle at T, chord BA is produced to meet the tangent at P. Perpendicular BC bisects the chord TA at C. If PA = 9 cm and TB = 7 cm, find the lengths of:
- AB
- PT
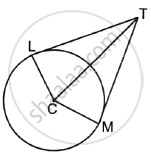
If two tangents TL and TM are drawn to a circle with centre C such that ∠LTM = 70°, then find ∠MCT.
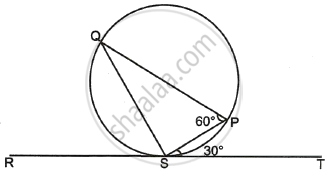
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.