Advertisements
Advertisements
Question
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is ______.
Options
12 cm
13 cm
8.5 cm
`sqrt119` cm
Solution
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is `bbunderline(sqrt119 cm)`.
Explanation:
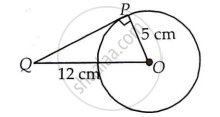
Suppose there is a circle whose center is O.
In right ΔQPO,
According to Pythagoras theorem,
OQ2 = OP2 + PQ2
= PQ = `sqrt(OQ^2 - OP^2)`
= PQ = `sqrt(12^2 - 5^2)`
= PQ = `sqrt(144 - 25`
= PQ = `sqrt119` cm.
APPEARS IN
RELATED QUESTIONS
In the figure given below, PQ is a chord of a circle with centre O and PT is a tangent. If ∠QPT = 60°, find ∠PRQ.

Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
How many tangents can a circle have?
A line intersecting a circle in two points is called a ______.
In the given figure O is the centre of the circle. Tangents A and B meet at C. If ∠ACO = 30°, find
1) ∠BCO
2) ∠AOB
3) ∠APB
In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

In the given Figure, AB and AC are tangents to the circle with centre O such that ∠BAC = 40°. Then ∠BOC is equal to ______
Out of the two concentric circles, the radius of the outer circle is 5 cm and the chord AC of length 8 cm is a tangent to the inner circle. Find the radius of the inner circle.
ABC is a right triangle with angle B = 90º. A circle with BC as diameter meets by hypotenuse AC at point D. Prove that: BD2 = AD × DC.
Construct a tangent to a circle with centre O and radius 3.5 cm at a point P on it.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
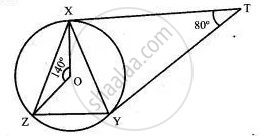
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
Find the value of ∠DCE.

The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.

In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

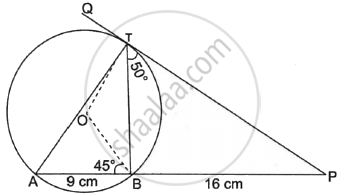
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT