Advertisements
Advertisements
Question
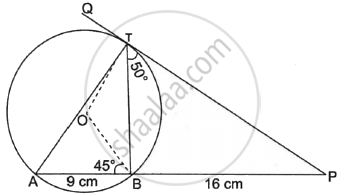
In the given figure, O is the centre of the circle. PQ is a tangent to the circle at T. Chord AB produced meets the tangent at P.
AB = 9 cm, BP = 16 cm, ∠PTB = 50° ∠OBA = 45°
Find:
- Length of PT
- ∠BAT
- ∠BOT
- ∠ABT
Solution
a.
PT2 = AP × BP
= (AB + BP) × BP
= (9 + 16) × 16
= 25 × 16
= 400
∴ PT = `sqrt(400)`
= 20 cm
b. Angles in alternate segments are equal
∴ ∠BAT = ∠PTB
= 50°
c. OT ⊥ PQ
∴ ∠OTP = 90°
`\implies` ∠OTP + ∠PTB = 90°
`\implies` ∠OTB + ∠50° = 90°
`\implies` ∠OTB = 90° – 50° = 40°
Now, In ΔBOT,
OB = OT(Radii of same circle)
∠OTB = ∠OBT = 40°
and ∠BOT + ∠OTB + ∠OBT = 180°
∠BOT + 40° + 40° = 180°
∠BOT = 180° – 80°
= 100°
d. In ΔABT,
∠ABT = ∠OBA + ∠OBT
= 45° + 40°
= 85°
APPEARS IN
RELATED QUESTIONS
In Fig. 7, two equal circles, with centres O and O’, touch each other at X. OO’ produced meets the circle with centre O’ at A. AC is tangent to the circle with centre O, at the point C. O’D is perpendicular to AC. Find the value of `(DO')/(CO')`

Prove that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
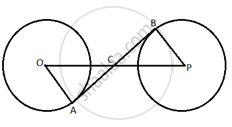
In the following fig. , AC is a transversal common tangent to tvvo circles with centres P and Q and of radii 6cm and 3cm respectively. Given that AB = 8cm, calculate PQ.
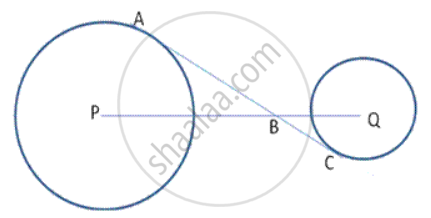
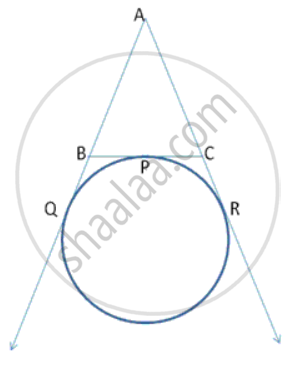
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
Two circle with radii r1 and r2 touch each other externally. Let r be the radius of a circle which touches these two circle as well as a common tangent to the two circles, Prove that: `1/sqrtr + 1/sqrtr_1 + 1/sqrtr_2`.
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.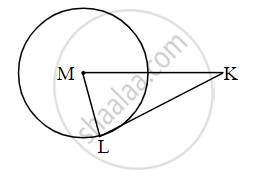
The distance between the centres of equal circles each of radius 3 cm is 10 cm. The length of a transverse tangent AB is ______
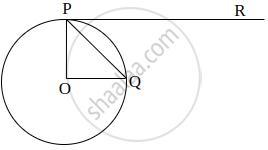
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

If O is centre of a circle and Chord PQ makes an angle 50° with the tangent PR at the point of contact P, then the angle subtended by the chord at the centre is ______.
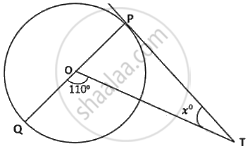
In the adjoining diagram, O is the centre of the circle and PT is a tangent. The value of x is ______.