Advertisements
Advertisements
Question
In the given figure, XAY is a tangent to the circle centered at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.

Solution

Given, ∠ABO = 40°
∠XAO = 90° ...(Angle between radius and tangent)
OA = OB ...(Radii of same circle)
⇒ ∠OAB = ∠OBA
∴ ∠OAB = 40°
Now, applying the linear pair of angles property,
we get
∠BAY + ∠OAB + ∠XAO = 180°
⇒ ∠BAY + 40° + 90° = 180°
⇒ ∠BAY + 130° = 180°
⇒ ∠BAY = 180° – 130°
⇒ ∠BAY = 50°
Now, In ΔAOB,
∠AOB + ∠OAB + ∠OBA = 180°
or, ∠AOB + 40° + 40° = 180°
or, ∠AOB = 180° – 80° = 100°
APPEARS IN
RELATED QUESTIONS
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP
AB is a diameter and AC is a chord of a circle with centre O such that ∠BAC = 30°. The tangent at C intersects extended AB at a point D. Prove that BC = BD.
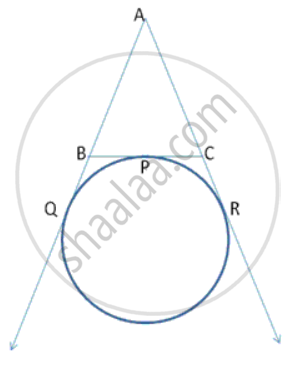
In following fig., a circle is touching the side BC of Δ ABC at P and AB and AC produced at Q and R respectively. Prove that AQ is half the perimeter of Δ ABC.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find AB.

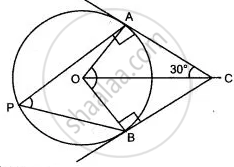
In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO = 30°,
find: (i) ∠ BCO (ii) ∠ AOB (iii) ∠ APB
The distance between two parallel tangents of a circle of radius 4 cm is ______
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ = 65°, then ∠BCD is ______


In the above figure, seg AB and seg AD are tangent segments drawn to a circle with centre C from exterior point A, then prove that: ∠A = `1/2` [m(arc BYD) - m(arc BXD)]
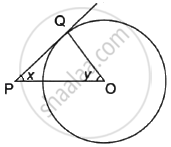
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
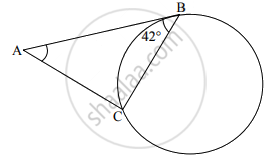
In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of ∠BAC is ______.
