Advertisements
Advertisements
Question
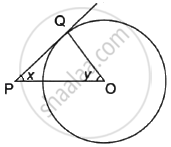
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is ______.
Options
45°
90°
60°
180°
Solution
In the given figure, PQ is a tangent to the circle with centre O. If ∠OPQ = x, ∠POQ = y, then x + y is 90°.

Explanation:
Given, ∠OPQ = x, ∠POQ = y
∠OQP = 90° ...(∵ Radius is perpendicular to the tangent at the point of contact.)
In ΔOPQ,
∠OPQ + ∠POQ + ∠OQP = 180° ...(angle sum property)
`\implies` x + y + 90° = 180°
`\implies` x + y = 180° – 90° = 90°
RELATED QUESTIONS
A line intersecting a circle in two points is called a ______.
A circle can have ______ parallel tangents at the most.
In triangle PQR, PQ = 24 cm, QR = –7 cm and ∠PQR = 90°. Find the radius of the inscribed circle.

In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In a square ABCD, its diagonal AC and BD intersect each other at point O. The bisector of angle DAO meets BD at point M and bisector of angle ABD meets AC at N and AM at L. Show that - ALOB is a cyclic quadrilateral.
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
Two equal chords AB and CD of a circle with center O, when produced meet at a point E, as shown in Fig. Prove that BE = DE and AE = CE.

Draw a circle of radius 2.7 cm and draw a chord PQ of length 4.5 cm. Draw tangents at points P and Q without using centre.
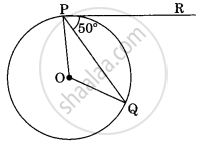
In figure, if O is the centre of a circle PQ is a chord and the tangent PR at P makes an angle of 50° with PQ, then ∠POQ is equal to ______.
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______