Advertisements
Advertisements
Question
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
Solution
We shall prove that ∠ACP = ∠BCP = 90°
and AC = BC
Now, ∠APC = ∠BPC
Since O lies on the bisector of ∠APB.
Δs ACP and BCP are congruent triangles by SAS congruence criterion,
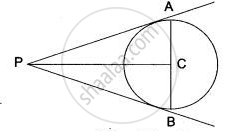
∴ AC = BC
and ∠ ACP = ∠ BCP
Since ∠ ACP + ∠ BCP = 180°
2 ∠ ACP = 180°
∠ ACP = 90°
∠ACP = ∠BCP = 90°
Hence proved.
APPEARS IN
RELATED QUESTIONS
A tangent to a circle intersects it in ______ point (s).
In the following figure, O is the centre of the circle and AB is a tangent to it at point B. ∠BDC = 65°. Find ∠BAO.
Show that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In Figure 3, a right triangle ABC, circumscribes a circle of radius r. If AB and BC are of lengths of 8 cm and 6 cm respectively, find the value of r.

Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
In figure, M is the centre of the circle and seg KL is a tangent segment. If MK = 12, KL = `6sqrt(3)`, then find
(i) Radius of the circle.
(ii) Measures of ∠K and ∠M.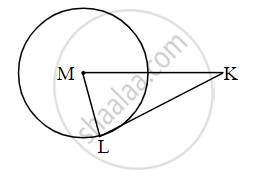
In the following figure, PA and PB are tangents from a point P to a circle with centre O. Then the quadrilateral OAPB must be a ______

The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to ______.

In the adjoining figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 30°, find the value of x.

