Advertisements
Advertisements
Question
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
Solution
Join OB and OC.
In Δ OBD and Δ OCD, we have
OB = OC ....(Each equal to the radius of circumcircle)
∠ODB = ∠ODC ....(Each equal to 90°)
and OD = OD ....(Common)
∴ Δ OBD ≅ Δ OCD
⇒ ∠BOD = ∠COD
⇒ ∠BOC = 2∠BOD = 2∠COD
Now, arc BC substends ∠BOC at the centre and ∠BAC = ∠A at a point in the remaining part of the circle.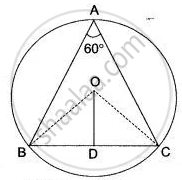
∴ ∠BOC = 2∠A
⇒ 2∠BOD = 2∠A ....( ∵∠BOC = 2∠BOD)
⇒ ∠BOD = ∠A
Hence proved.
APPEARS IN
RELATED QUESTIONS
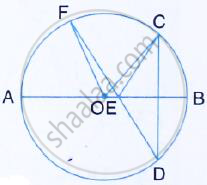
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
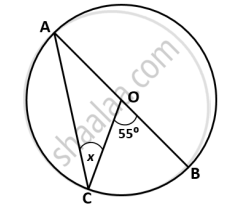
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.
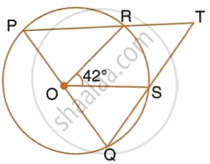
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS.
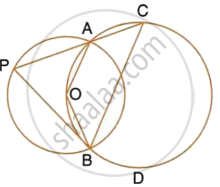
In the given figure, AB is the diameter of the circle with centre O.
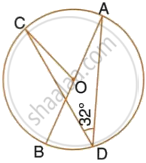
If ∠ADC = 32°, find angle BOC.
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
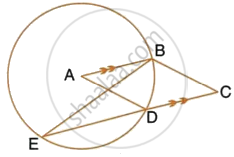
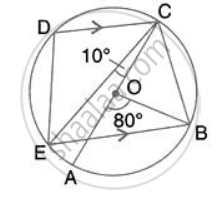
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
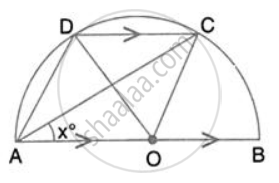
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DOC.
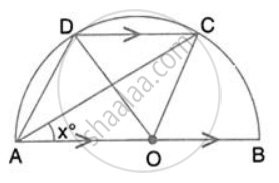
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DAC
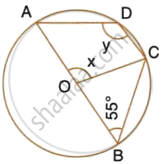
In the given figure, AB is a diameter of the circle with centre ‘O’. If ∠COB = 55⁰ then the value of x is: