Advertisements
Advertisements
Question
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DAC
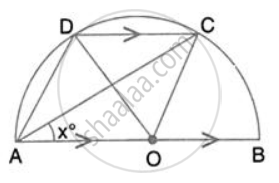
Solution
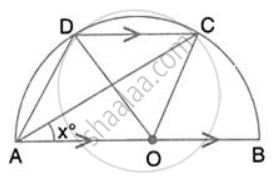
∠DAC = `1 /2 ` ∠DOC = `1/2 (180° - 4x ) = 90° - 2x `
(Angle at the centre is double the angle at the circumference subtended by the same chord)
APPEARS IN
RELATED QUESTIONS
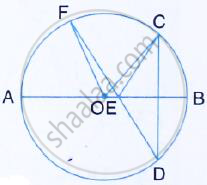
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
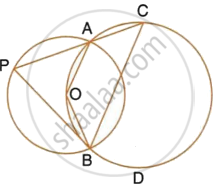
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : obtuse ∠AOB,
Give reasons for your answers clearly.
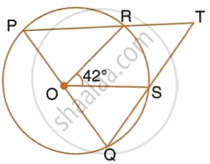
In the given figure, PQ is the diameter of the circle whose centre is O. Given ∠ROS = 42°, calculate ∠RTS.
In a regular pentagon ABCDE, inscribed in a circle; find ratio between angle EDA and angle ADC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ DBC
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ABD
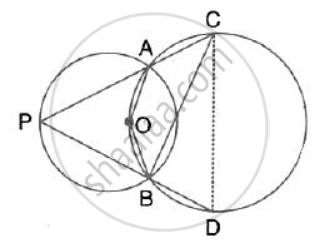
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ADB

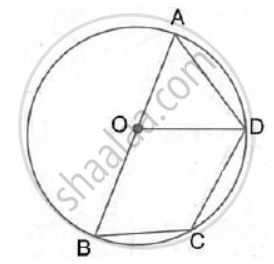
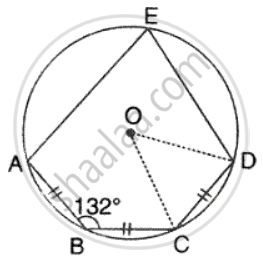
In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠ COD.
Prove that the line segment joining the midpoints of two equal chords of a circle subtends equal angles with the chord.
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
