Advertisements
Advertisements
Question
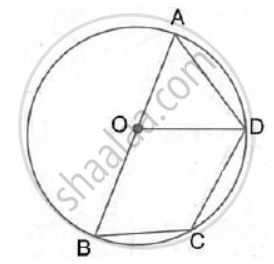
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ DBC
Solution

∠BDA = 90° (Angle in a semicircle)
Also, ∠OAD is equilateral (∴ ∠OAD = 60° )
∴ ∠ODB = 90° - ∠ODA = 90° - 60° = 30°
Also, OD || BC
∴ ∠DBC = ∠ODB = 30° (Alternate angles)
APPEARS IN
RELATED QUESTIONS
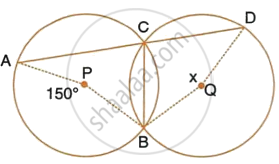
In the figure, given below, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x .
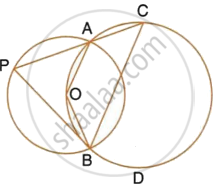
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : obtuse ∠AOB,
Give reasons for your answers clearly.
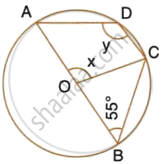
In the given figure, O is the centre of the circle and ∠ABC = 55°. Calculate the values of x and y.
The figure given below, shows a circle with centre O. Given : ∠AOC = a and ∠ABC = b.
-
Find the relationship between a and b.
-
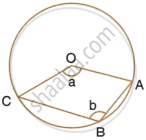
Find the measure of angle OAB, if OABC is a parallelogram.
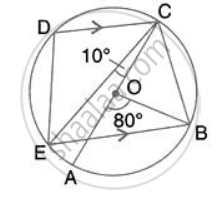
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
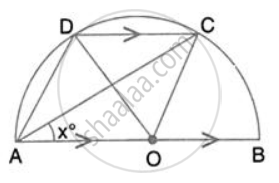
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DAC
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ADB

In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠AED

In a circle with center O, chords AB and CD intersect inside the circumference at E. Prove that ∠ AOC + ∠ BOD = 2∠ AEC.
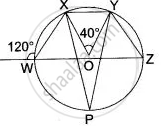
In the figure alongside O is the centre of circle ∠ XOY = 40°, ∠ TWX = 40° and XY is parallel to TZ.
Find: (i) ∠ XZY, (ii) ∠ YXZ (iii) ∠ TZY.