Advertisements
Advertisements
Question
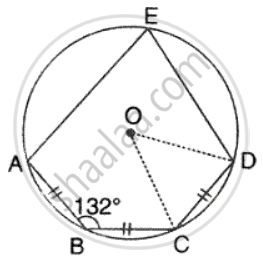
In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠AED

Solution

In the figure, O is the centre of circle, with AB = BC = CD.
Also, ∠ABC = 132°
Similarly, AB = BC = CD
∠AEB = ∠BEC = ∠CED = 24°
∠AED = ∠AEB + ∠BEC + ∠CED
= 24° + 24° + 24°= 72°
APPEARS IN
RELATED QUESTIONS
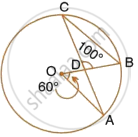
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.
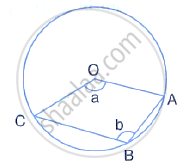
The figure given below, shows a Circle with centre O.
Given: ∠AOC = a and ∠ABC = b.
Find the relationship between a and b
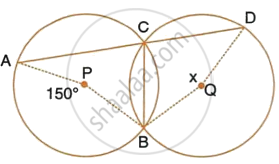
In the figure, given below, P and Q are the centres of two circles intersecting at B and C. ACD is a straight line. Calculate the numerical value of x .
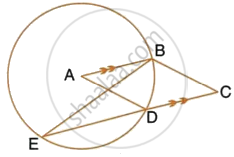
In the given figure, A is the centre of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠CAB
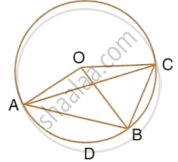
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
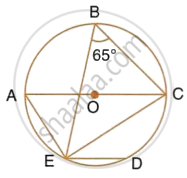
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DOC.
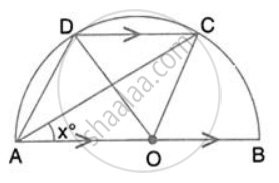
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ADB

In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠ COD.
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
