Advertisements
Advertisements
Question
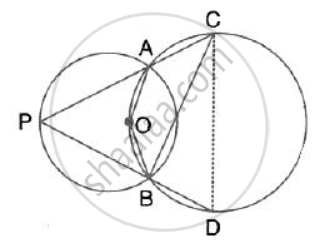
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ABD
Solution
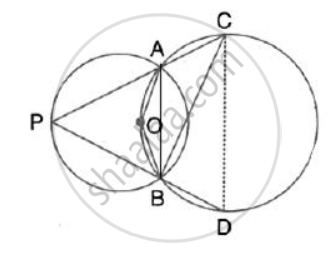
Join AB and AD
In cyclic quadrilateral ABDC
∠ABD = 180° - ∠ACD = 180° - (40° + 30° ) = 110°
(pair of opposite angles in a cyclic quadrilateral are supplementary)
APPEARS IN
RELATED QUESTIONS
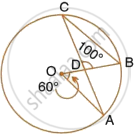
In the following figure, O is the centre of the circle, ∠AOB = 60° and ∠BDC = 100°. Find ∠OBC.
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
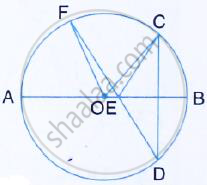
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
- ∠ABD,
- ∠DBC,
- ∠ADC.
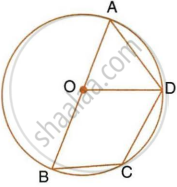
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find: ∠CAB
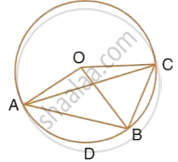
In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ACB,
Give reasons for your answers clearly.
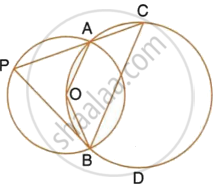
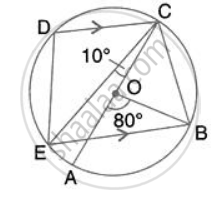
In the given figure, AC is the diameter of circle, centre O. CD and BE are parallel. Angle AOB = 80o and angle ACE = 10o. Calculate: Angle CED.
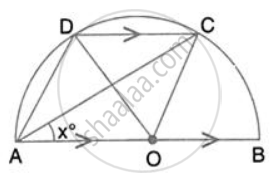
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ ADC.
If O is the circumcentre of a Δ ABC and OD ⊥ BC, prove that ∠ BOD = ∠A.
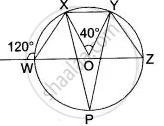
In the figure alongside O is the centre of circle ∠ XOY = 40°, ∠ TWX = 40° and XY is parallel to TZ.
Find: (i) ∠ XZY, (ii) ∠ YXZ (iii) ∠ TZY.