Advertisements
Advertisements
प्रश्न
If PA and PB are two tangents drawn from a point P to a circle with center C touching it A and B, prove that CP is the perpendicular bisector of AB.
उत्तर
We shall prove that ∠ACP = ∠BCP = 90°
and AC = BC
Now, ∠APC = ∠BPC
Since O lies on the bisector of ∠APB.
Δs ACP and BCP are congruent triangles by SAS congruence criterion,
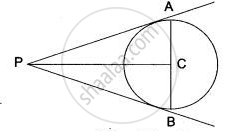
∴ AC = BC
and ∠ ACP = ∠ BCP
Since ∠ ACP + ∠ BCP = 180°
2 ∠ ACP = 180°
∠ ACP = 90°
∠ACP = ∠BCP = 90°
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

In Figure 2, XP and XQ are two tangents to the circle with centre O, drawn from an external point X. ARB is another tangent, touching the circle at R. Prove that XA + AR = XB + BR ?

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
A chord of a length 16.8 cm is at a distance of 11.2 cm from the centre of a circle . Find the length of the chord of the same circle which is at a distance of 8.4 cm from the centre.
In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find the length of tangent PT.

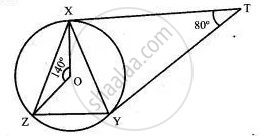
In the alongside, figure, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°. Calculate the value of ∠ZXY.
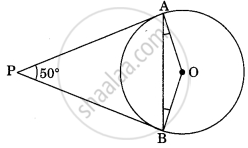
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to ______.
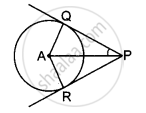
In the figure, PQ and PR are tangents to a circle with centre A. If ∠QPA=27°, then ∠QAR equals to ______
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
