Advertisements
Advertisements
Question
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
Solution
Given the distance between two tangents parallel to each other to a circle is 13 cm.
Two parallel tangents to a circle are found when the line joining the point of contact are diameter.
∴ d = 13 cm
Since, r = `d/2 = 13/2` = 6.5 cm
Hence, radius of circle is 6.5 cm.
APPEARS IN
RELATED QUESTIONS
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
In the given figure, find TP if AT = 16 cm and AB = 12 cm.

Four alternative answers for the following question is given. Choose the correct alternative.
If two circles are touching externally, how many common tangents of them can be drawn?
Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
If Δ ABC is isosceles with AB = AC and C (O, r) is the incircle of the ΔABC touching BC at L,prove that L bisects BC.
In the following figure, PQ is the tangent to the circle at A, DB is a diameter and O is the centre of the circle. If ∠ ADB = 30° and ∠ CBD = 60° ; calculate : ∠CDB

In the given figure, O is the centre of the circle. Tangents at A and B meet at C. If angle ACO = 30°, find: angle AOB

In Fig. TA is a tangent to a circle from the point T and TBC is a secant to the circle. If AD is the bisector of ∠BAC, prove that ΔADT is isosceles.

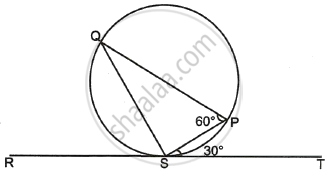
In the given diagram RT is a tangent touching the circle at S. If ∠PST = 30° and ∠SPQ = 60°, then ∠PSQ is equal to ______.
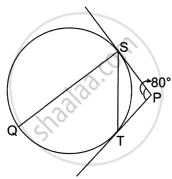
In the given diagram, PS and PT are the tangents to the circle. SQ || PT and ∠SPT = 80°. The value of ∠QST is ______.